「杂题记录」括号序列（格路计数）

给出两个正整数 \(n, k\) 。

求出有多少个长度为 \(n\) 的括号序列，满足最长合法括号子序列长度恰好为 \(2k\) 。

分析

根据卡特兰数的转化同样可以对这个问题进行转化。

可以发现如果前缀和为 \(S_i\) ，那么最长的合法括号子序列长度为 \(n-S_n + 2\min\{S\}\)，注意 \(min\{S\}\)通常为负值。

example.png

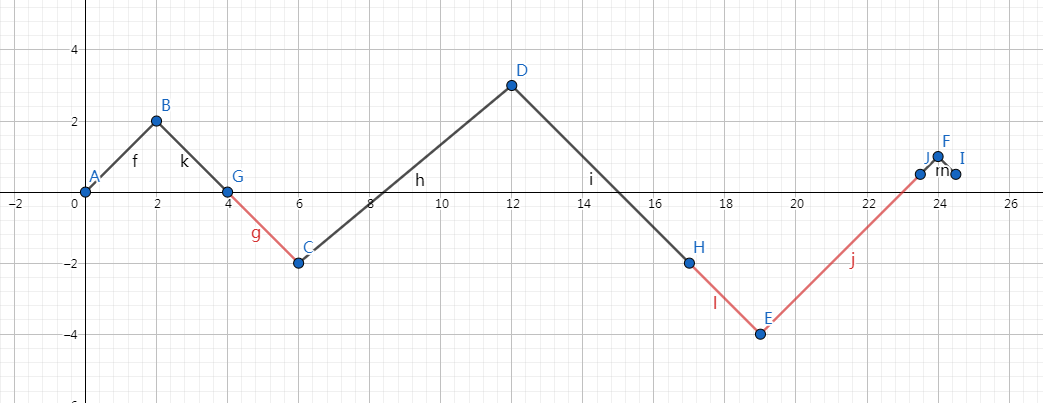
其中红色的线段为无效符号，E 为最低点。

设 \(t=\min\{S\}\)，易知 \(S_n = n+2t+2k\)。

可以考虑枚举 \(t\) ，问题就变成了格路计数，需要满足一定到达过 \(y=t\) 这个直线，且未曾穿过。

未曾穿过的限制可以考虑用卡特兰数的推导相同的思想，即翻折引理。

到达过这条线的要求可以考虑用 \(\min\{S\} \ge t\) 的答案减去 \(\min\{S\} > t\) 的答案得到。

考虑不经过 \(y=t-1\) 时的答案：（根据翻折引理） \[ \dbinom{n}{(n-S_n)/2}-\dbinom{n}{\left[n - (2(t-1)-S_n)\right]/2}=\dbinom{n}{k-t}-\dbinom{n}{k-1} \] 同理，不经过 \(y=t\) 的答案为： \[ \dbinom{n}{k-t}-\dbinom{n}{k} \]

做差发现是： \[ \dbinom{n}{k-1}-\dbinom{n}{k} \] 有不等式 \(S_n \ge \min\{S\}\)，易知：\(t \ge 2k-n\).即 \(k\) 有 \(n-2k+1\) 种取值。

答案为： \((n+1-2k)\left(\dbinom{n}{k}-\dbinom{n}{k-1}\right)\)

这应该就能做到线性了，如果有个小巧的质数就能做到更快了。