两个重要函数
CNN 可以视作以下两个函数的集合.
得分函数 (Score Function)
\(f(\vec{x}; W)\).其中 \(\vec{x}\) 为输入网络的数据,\(W\) 为网络中的所有参数.本质上参数是网络的固有特性.
得分函数可以简单理解为输入一个向量,输出一个向量的函数,输出的向量为的第 \(i\) 维,为第 \(i\) 种类别的得分.
得分函数是整个神经网络的抽象.
损失函数 (Loss Function)
用于衡量 得分函数 给分 的优劣程度.损失 (Loss) 是相对于某组特定的 数据 来说的.
对于 CNN 数据 可以抽象为 输入数据 (input) \(\{\vec{x_i}\}\) 和 标签 (label) \(\{y_i\}\),其中 输入数据 和 标签 一一对应,设长度为 \(N\),损失函数可以定义为 \(L(W; \{\vec{x_i}\}, \{y_i\})\).
有不同的若干种常见的 损失函数 的定义方式:
Multiclass Support Vector Machine loss
\[ L_i(W; \vec{x_i}, y_i) = \sum_{j\not=y_i}\max{(0, f(\vec{x_i};W)_j - f(\vec{x_i};W)_{y_i} + \Delta)} \] 其中 \(L_i\) 为对于第 \(i\) 组数据的 "损失". \(\Delta\) 为 超参数 (Hyperparameter) 可以理解为期望下第 \(y_i\) 类得分的显著性水平。

对于整体损失还需要加入 正则损失 (Regularization Loss) 项,正则损失定义为 \[ R(W) = \begin{cases} \sum_{i, j, k, \cdots} (W_{i, j, k, \cdots})^2 & \text{L2 Regularization} \\ \sum_{i, j, k, \cdots} |W_{i, j, k, \cdots}| & \text{L1 Regularization} \\ \sum_{i, j, k, \cdots} \beta(W_{i, j, k, \cdots})^2 + |W_{i, j, k, \cdots}| & \text{Elastic Net Regularization} \\ \end{cases} \] 主要为了鼓励参数稀疏,减轻模型复杂度,在一定程度上减轻过拟合。
对于一组数据 \(\{\vec{x_i}\}, \{y_i\}\) 其 整体损失函数 \(L\left(W, \{\vec{x_i}\}, \{y_i\}\right)\) 的定义为: \[ L\left(W; \{\vec{x_i}\}, \{y_i\}\right)=\frac{1}{N}\sum_{i}L_i + \alpha R(W) \] 其中 \(\alpha\) 为超参数。
Softmax Loss
定义为: \[ L_i(W; \vec{x_i}, y_i) = -\log\left(\frac{\exp{f(\vec{x_i};W)_{y_i}}}{\sum_{j}\exp{f(\vec{x_i};W)_{j}}}\right)=-f(\vec{x_i};W)_{y_i}+\log\left(\sum_{j}\exp{f(\vec{x_i};W)_{j}}\right) \]
一个计算上的技巧是,可以对 \(f(\vec{x_i};W) \leftarrow f(\vec{x_i}; W) - \max_j{\{f(\vec{x_i};W)\}_j}\),在计算上 \(L_i\) 结果不变. 可以防止 \(\exp\) 计算是函数值过大导致溢出。
其 整体损失函数 的定义和上述相同。 \[ L\left(W; \{\vec{x_i}\}, \{y_i\}\right)=\frac{1}{N}\sum_{i}L_i + \alpha R(W) \]
两种计算 Loss 的主要方法没有明显优势劣势。
- 对于 SVM Loss ,其目标是 正确类别 的得分要高于 其他类比 一个特定值即可。如果高于之后就不会对模型产生影响。
- 对于 Softmax Loss,他会不断使得模型增加 正确类别 得分的显著性。
SVM Loss 可能会把更多的精力放在相似类别分辨的细化上
CS231n note 原文
For example, a car classifier which is likely spending most of its “effort” on the difficult problem of separating cars from trucks should not be influenced by the frog examples, which it already assigns very low scores to, and which likely cluster around a completely different side of the data cloud. (cs231n, 2024).
Loss 函数可以可视化
若其输入的参数量为 \(N\),则考虑在 \(N\) 维空间中取一平面,生成 Loss 值在这一平面上的 heatmap.具体考虑生成两随机向量 \(\vec{W_1}, \vec{W_2}\),和一个随机平面中心点 \(W\),定义 \[ l'(a, b) = L\left(W + aW_1+ bW_2; \{\vec{x_i}\}, \{y_i\}\right)\]
绘制 \(l'(a, b)\) 的热图即可。
优化 (Optimization)
通过调整参数的取值,使得整个网络的 Loss 值更低。
本质是数值方法优化多变量函数,可以使用梯度下降法(Stochastic Gradient Descent)。梯度 \(\nabla_{w}L\) ,可以在每次算出 Loss 的时候通过反向传播求出 (Back Propagation)。
- 正向过程(Forward):从网络第一层出发,代入网络每一层网络,最终计算出结果向量和 Loss 值。
- 反向过程(Backword):从 Loss 值出发,利用 Chain Rule 推知 \(\nabla_{W}L\)。
神经网络结构 (Architecture)
神经网络的计算传递结构本质上是一个 DAG (Directed Acyclic Graph).
神经元
数学上定义为一个多自变量函数。如神经元输入量为 \(n\),第 \(i\) 个突触的输入数据为 \(x_i\) 则: \[ \sigma\left(\sum_{i}^{n}{w_ix_i} + b\right) \] 其中 \(\sigma(x)\) 为激活函数。
As Linear Classifier
单个神经元可以当成一个 线性分类器 因为从激活函数的角度观察,神经元有能力喜欢或者不喜欢某种信号,即 激活函数 存在阈值。
常用激活函数
- Sigmoid / tanh 不太行。
- ReLU (Rectified Linear Unit): \(f(x) = \max(0, x)\) 当训练学习率(Learning Rate)过大导致其参数变化过大,会使得其永远不可能被激活,导致神经元死亡 (Dying ReLU)。 可以通过调小 Learning Rate 规避。
- Leaky ReLU:\(f(x) = [x < 0](\alpha x) + [x \ge 0]x\) 可能对 Dying ReLU 有帮助。
- Maxout: \(f(x) = (w_1x+b_1, w_2x+b_2)\),其实是 ReLU 和 Leaky ReLU,综合了 ReLU 的优点,规避了其缺点。但是增加了参数数量
选择策略: - 可以优先考虑 ReLU. 但是要设置合理的 Learning Rate - 如果其效果不好,可以试一下 Leaky ReLU 和 Maxout. - 别用 Sigmoid,慎用 tanh
表现力(Representational Power)
具有一层以上 隐藏层(Hidden Layer)的 训练好的 神经网络 \(g(x)\),对于任意 \(f(x)\),有: \[ \forall x\ \forall \epsilon>0, \left|f(x)-g(x)\right| < \epsilon \] 对于一层以上的神经网络在数学上可以表示任何函数。
但是实践中使用层数较多的神经网络有更多优势,如便于训练和理解。
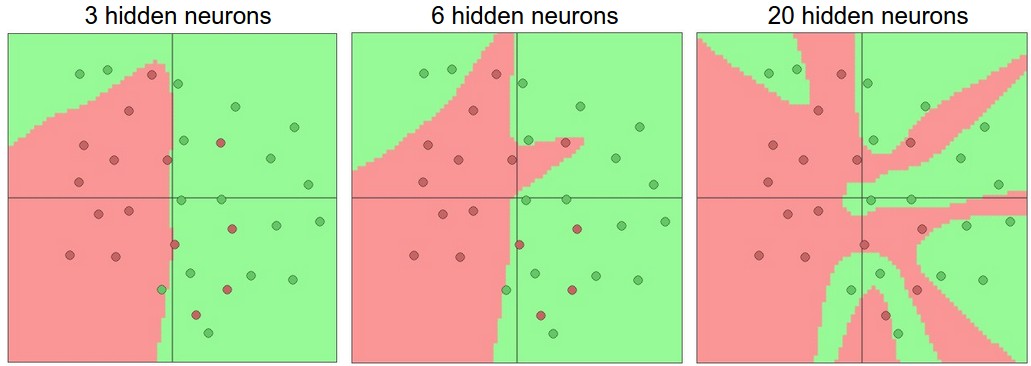
模型的实际表现能力也会随层数增多而增强。
层数过多确实会在训练中造成过拟合的风险,但是减少层数不是缓解过拟合的方法,后面会有更常用的减轻过拟合的方法,例如提高正则系数(Regularization Rate) \(\alpha\)
对于全连接神经网络,当层数大于 \(3\) 时,增加层数带来的表现力的增加收益会减轻。 但是对于 CNN 却不是这样,CNN 层数增加往往都能换来更强的神经网络表现力。
数据预处理(Data Pre-Processing)
- 中心化(Mean subtraction):使得数据 zero-centered \(\vec{x} \leftarrow (\vec{x} - \text{mean}{(\vec{x})})\)
- 正态化(Normalization ): 使得中心化后的数据服从正态分布 \(\vec{x} \leftarrow (\vec{x}\ / \ \text{std}{(\vec{x})})\)。 一般是对于单位不同的数据进行处理,CNN 中对于图像来说,影响不大。
- PCA 和 白化(Whitening): 略 没看懂
权值初始化(Weight Initialization)
设 \(X \sim(N(0, 1))\)
一种很好的初始化方法为,使权值 \(W_i \leftarrow X / \sqrt{n}\) 其中 \(n\) 为上一层的节点数。
对于使用 ReLU 的网络,一种效果更好的初始化方法为,使权值 \(W_i \leftarrow X \times \sqrt{2/n}\) 其中 \(n\) 为上一层的节点数。
考虑积极使用 Batch Normalization 能够极大的增加权值初始化的鲁棒性。
正则化(Regularization)
防止网络过拟合。
L2 regularization
L1 regularization
Max norm constraints:强制设置参数上界
Dropout:使得每次训练的时候强制部分神经元不激活,假设激活某一个特定神经元的概率为 \(p\)
两种方法:
- Dropout 训练时按 \(p\) 的概率激活神经元,预测时每层节点数值扩大到 \(1/p\) 倍。
- Inverted Dropout,训练时按 \(p\) 的概率激活神经元,并且将节点数值扩大到 \(1/p\) 倍,预测时正常计算。
实践中更常用的方法是:L2 Regularization。 如果过拟合严重,考虑 Inverted Dropout (\(p=0.5\))
损失函数(Loss Function)
对于 Batch Train,损失函数的定义一般为 \(L=\frac{1}{N}\sum_{i}L_i\).
对于种类较多的 Loss Function,计算 Softmax 开销较大。可以尝试采用 https://arxiv.org/pdf/1310.4546.pdf 中的方法。
对于属性分类(Attribute classification),Loss 函数有特殊的定义方式,Attribute classification
对于回归(Regression)任务,可以用来预测特定的值。Loss 函数可以简单定义为 \(L_i = (f-y_i)^2\)
关于 Loss 函数选取的一些注意事项
L2 Loss 相比于 Softmax 等 Loss 函数稳定性较差。 L2 Loss 很容易会引起很大的梯度。在归类问题中慎用 Loss Function
回归问题的一些注意 CS231N 原文
When faced with a regression task, first consider if it is absolutely necessary. Instead, have a strong preference to discretizing your outputs to bins and perform classification over them whenever possible.