给出两个正整数
n,k
。
求出有多少个长度为
n
的括号序列,满足最长合法括号子序列长度恰好为
2k
。
分析
根据卡特兰数的转化同样可以对这个问题进行转化。
可以发现如果前缀和为
Si
,那么最长的合法括号子序列长度为
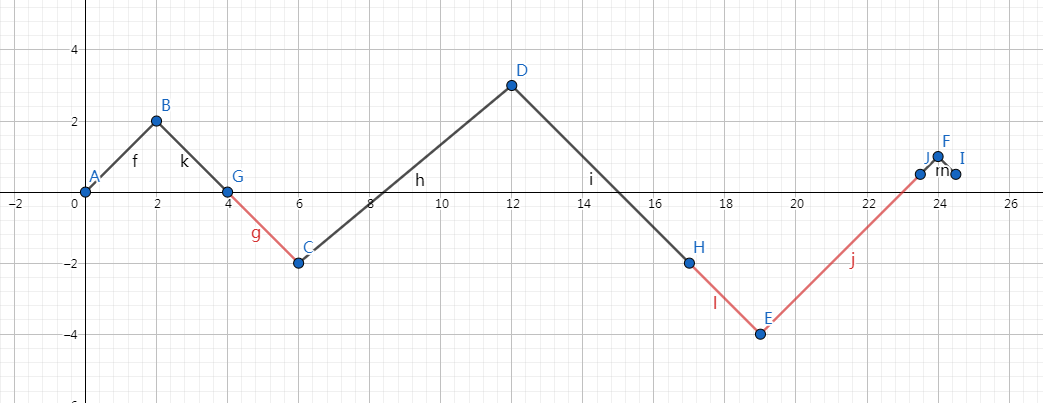
n−Sn+2min{S},注意
min{S}通常为负值。
 example.png
example.png
其中红色的线段为无效符号,E 为最低点。
设
t=min{S},易知
Sn=n+2t+2k。
可以考虑枚举
t
,问题就变成了格路计数,需要满足一定到达过
y=t
这个直线,且未曾穿过。
未曾穿过的限制可以考虑用卡特兰数的推导相同的思想,即翻折引理。
到达过这条线的要求可以考虑用
min{S}≥t
的答案减去
min{S}>t
的答案得到。
考虑不经过
y=t−1
时的答案:(根据翻折引理)
((n−Sn)/2n)−([n−(2(t−1)−Sn)]/2n)=(k−tn)−(k−1n)
同理,不经过
y=t
的答案为:
(k−tn)−(kn)
做差发现是:
(k−1n)−(kn)
有不等式
Sn≥min{S},易知:t≥2k−n.即
k
有
n−2k+1
种取值。
答案为:
(n+1−2k)((kn)−(k−1n))
这应该就能做到线性了,如果有个小巧的质数就能做到更快了。
🔗 Source Hash:
584bacf2b75962ad49d72b2b4812b9ef2abb1ed932558b4e92a8e8daa3161cbd
Build Logs
Build Log - Filtered
================================================
📋 Information:
• Path information has been filtered for privacy protection
• File names are preserved for debugging purposes
• All build status and error messages are kept intact
🔍 Filter Rules:
• /absolute/path/file.ext → .../file.ext
• /home/username → .../[user]
• /tmp/files → .../[temp]
• /usr/share/packages → .../[system]
================================================
html log:
CMD: ['pandoc', '-s', 'cache/oi-blog_「杂题记录」括号序列(格路计数).md', '--filter', 'pandoc-crossref', '--filter', 'pandoc-katex', '--template=cache/pandoc_html_template.html', '-o', 'cache.../oi-blog_「杂题记录」括号序列(格路计数).md.html', '--metadata', '--verbose', '--highlight-style=tango']
STDOUT:
STDERR: WARNING: pandoc-crossref was compiled with pandoc 3.6.2 but is being run through 3.6.4. This is not supported. Strange things may (and likely will) happen silently.
====================================================================================================
pdf log:
CMD: ['pandoc', '-s', 'cache.../cac35d1d25.pdf.md', '-o', 'cache/cac35d1d25.pdf', '-H', 'static/pandoc.header.tex', '--pdf-engine=xelatex', '--verbose']
STDOUT:
STDERR: [INFO] Loaded static.../pandoc.header.tex from static.../pandoc.header.tex
[INFO] Fetching https://i.loli.net/2021/01/27/7Bt4EbCKUVjGYgH.png...
[INFO] Extracting .../[temp]
[INFO] Not rendering RawInline (Format "html") ""
[INFO] [makePDF] Temp dir:
.../[temp]
[INFO] [makePDF] Command line:
xelatex "-halt-on-error" "-interaction" "nonstopmode" "-output-directory" ".../[temp] ".../[temp]
[INFO] [makePDF] Relevant environment variables:
("TEXINPUTS",".../[temp]
("TEXMFOUTPUT",".../[temp]
("SHELL","/bin/bash")
("PWD",".../[user]/projects/blog")
("HOME",".../[user]
("LANG","zh_CN.UTF-8")
("PATH",".../[user]/.local/bin:.../[user]/.cargo/bin:.../[user]/miniconda3/envs/myblog/bin:.../[user]/miniconda3/condabin:.../[temp]
[INFO] [makePDF] Source:
% Options for packages loaded elsewhere
\PassOptionsToPackage{unicode}{hyperref}
\PassOptionsToPackage{hyphens}{url}
\PassOptionsToPackage{space}{xeCJK}
\documentclass[
]{article}
\usepackage{xcolor}
\usepackage[a4paper,margin=2cm]{geometry}
\usepackage{amsmath,amssymb}
\setcounter{secnumdepth}{-\maxdimen} % remove section numbering
\usepackage{iftex}
\ifPDFTeX
\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}
\usepackage{textcomp} % provide euro and other symbols
\else % if luatex or xetex
\usepackage{unicode-math} % this also loads fontspec
\defaultfontfeatures{Scale=MatchLowercase}
\defaultfontfeatures[\rmfamily]{Ligatures=TeX,Scale=1}
\fi
\usepackage{lmodern}
\ifPDFTeX\else
% xetex/luatex font selection
\setmainfont[]{Latin Modern Roman}
\ifXeTeX
\usepackage{xeCJK}
\setCJKmainfont[]{AR PL UKai CN}
\fi
\ifLuaTeX
\usepackage[]{luatexja-fontspec}
\setmainjfont[]{AR PL UKai CN}
\fi
\fi
% Use upquote if available, for straight quotes in verbatim environments
\IfFileExists{upquote.sty}{\usepackage{upquote}}{}
\IfFileExists{microtype.sty}{% use microtype if available
\usepackage[]{microtype}
\UseMicrotypeSet[protrusion]{basicmath} % disable protrusion for tt fonts
}{}
\usepackage{setspace}
\makeatletter
\@ifundefined{KOMAClassName}{% if non-KOMA class
\IfFileExists{parskip.sty}{%
\usepackage{parskip}
}{% else
\setlength{\parindent}{0pt}
\setlength{\parskip}{6pt plus 2pt minus 1pt}}
}{% if KOMA class
\KOMAoptions{parskip=half}}
\makeatother
\usepackage{graphicx}
\makeatletter
\newsavebox\pandoc@box
\newcommand*\pandocbounded[1]{% scales image to fit in text height/width
\sbox\pandoc@box{#1}%
\Gscale@div\@tempa{\textheight}{\dimexpr\ht\pandoc@box+\dp\pandoc@box\relax}%
\Gscale@div\@tempb{\linewidth}{\wd\pandoc@box}%
\ifdim\@tempb\p@<\@tempa\p@\let\@tempa\@tempb\fi% select the smaller of both
\ifdim\@tempa\p@<\p@\scalebox{\@tempa}{\usebox\pandoc@box}%
\else\usebox{\pandoc@box}%
\fi%
}
% Set default figure placement to htbp
\def\fps@figure{htbp}
\makeatother
\setlength{\emergencystretch}{3em} % prevent overfull lines
\providecommand{\tightlist}{%
\setlength{\itemsep}{0pt}\setlength{\parskip}{0pt}}
% \usepackage{xeCJK}
% \setCJKmainfont{AR PL UKai CN}
% \usepackage{unicode-math}
\setmathfont{Latin Modern Math}
\usepackage{bookmark}
\IfFileExists{xurl.sty}{\usepackage{xurl}}{} % add URL line breaks if available
\urlstyle{same}
\hypersetup{
pdftitle={「杂题记录」括号序列(格路计数)},
pdfauthor={Jiayi Su (ShuYuMo)},
hidelinks,
pdfcreator={LaTeX via pandoc}}
\title{「杂题记录」括号序列(格路计数)}
\author{Jiayi Su (ShuYuMo)}
\date{2021-01-19 15:35:06}
\begin{document}
\maketitle
\setstretch{1.3}
给出两个正整数 \(n, k\) 。
求出有多少个长度为 \(n\) 的括号序列,满足最长合法括号子序列长度恰好为
\(2k\) 。
\subsection{分析}\label{ux5206ux6790}
根据\href{./「琐记」卡特兰数}{卡特兰数的转化}同样可以对这个问题进行转化。
可以发现如果前缀和为 \(S_i\) ,那么最长的合法括号子序列长度为
\(n-S_n + 2\min\{S\}\),注意 \(min\{S\}\)通常为负值。
\begin{figure}
\centering
\pandocbounded{\includegraphics[keepaspectratio]{.../[temp]
\caption{example.png}
\end{figure}
其中红色的线段为无效符号,E 为最低点。
设 \(t=\min\{S\}\),易知 \(S_n = n+2t+2k\)。
可以考虑枚举 \(t\) ,问题就变成了格路计数,需要满足一定到达过 \(y=t\)
这个直线,且未曾穿过。
未曾穿过的限制可以考虑用\href{./「琐记」卡特兰数}{卡特兰数的推导}相同的思想,即翻折引理。
到达过这条线的要求可以考虑用 \(\min\{S\} \ge t\) 的答案减去
\(\min\{S\} > t\) 的答案得到。
考虑不经过 \(y=t-1\) 时的答案:(根据翻折引理) \[
\dbinom{n}{(n-S_n)/2}-\dbinom{n}{\left[n - (2(t-1)-S_n)\right]/2}=\dbinom{n}{k-t}-\dbinom{n}{k-1}
\] 同理,不经过 \(y=t\) 的答案为: \[
\dbinom{n}{k-t}-\dbinom{n}{k}
\]
做差发现是: \[
\dbinom{n}{k-1}-\dbinom{n}{k}
\] 有不等式 \(S_n \ge \min\{S\}\),易知:\(t \ge 2k-n\).即 \(k\) 有
\(n-2k+1\) 种取值。
答案为: \((n+1-2k)\left(\dbinom{n}{k}-\dbinom{n}{k-1}\right)\)
这应该就能做到线性了,如果有个小巧的质数就能做到更快了。
\end{document}
[INFO] [makePDF] LaTeX run number 1
[INFO] [makePDF] LaTeX output
This is XeTeX, Version 3.141592653-2.6-0.999995 (TeX Live 2023/Debian) (preloaded format=xelatex)
restricted \write18 enabled.
entering extended mode
(.../input.tex
LaTeX2e <2023-11-01> patch level 1
L3 programming layer <2024-01-22>
(.../article.cls
Document Class: article 2023/05/17 v1.4n Standard LaTeX document class
(.../[system]
(.../xcolor.sty
(.../color.cfg)
(.../xetex.def)
(.../[system]
(.../geometry.sty
(.../keyval.sty)
(.../ifvtex.sty
(.../iftex.sty)))
(.../amsmath.sty
For additional information on amsmath, use the `?' option.
(.../amstext.sty
(.../amsgen.sty))
(.../amsbsy.sty)
(.../amsopn.sty))
(.../amssymb.sty
(.../amsfonts.sty))
(.../unicode-math.sty
(.../expl3.sty
(.../l3backend-xetex.def))
(.../unicode-math-xetex.sty
(.../xparse.sty)
(.../l3keys2e.sty)
(.../fontspec.sty
(.../fontspec-xetex.sty
(.../fontenc.sty)
(.../fontspec.cfg)))
(.../fix-cm.sty
(.../ts1enc.def))
(.../unicode-math-table.tex)))
(.../lmodern.sty)
(.../xeCJK.sty
(.../ctexhook.sty)
(.../xtemplate.sty)
(.../xeCJK.cfg))
(.../upquote.sty
(.../textcomp.sty))
(.../microtype.sty
(.../etoolbox.sty)
(.../microtype-xetex.def)
(.../microtype.cfg))
(.../setspace.sty)
(.../parskip.sty
(.../kvoptions.sty
(.../ltxcmds.sty)
(.../kvsetkeys.sty)))
(.../graphicx.sty
(.../graphics.sty
(.../trig.sty)
(.../graphics.cfg)))
(.../bookmark.sty
(.../hyperref.sty
(.../kvdefinekeys.sty)
(.../pdfescape.sty
(.../pdftexcmds.sty
(.../infwarerr.sty)))
(.../hycolor.sty)
(.../auxhook.sty)
(.../nameref.sty
(.../refcount.sty)
(.../gettitlestring.sty))
(.../pd1enc.def)
(.../intcalc.sty)
(.../puenc.def)
(.../url.sty)
(.../bitset.sty
(.../bigintcalc.sty))
(.../atbegshi-ltx.sty))
(.../hxetex.def
(.../stringenc.sty)
(.../rerunfilecheck.sty
(.../atveryend-ltx.sty)
(.../uniquecounter.sty)))
(.../bkm-dvipdfm.def))
(.../xurl.sty)
No file input.aux.
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(.../mt-LatinModernRoman.cfg)
Package hyperref Warning: Rerun to get /PageLabels entry.
(.../omllmm.fd)
(.../umsa.fd)
(.../mt-msa.cfg)
(.../umsb.fd)
(.../mt-msb.cfg)
LaTeX Font Warning: Font shape `TU/ARPLUKaiCN(0)/b/n' undefined
(Font) using `TU/ARPLUKaiCN(0)/m/n' instead on input line 96.
[1] [2] (.../input.aux)
LaTeX Font Warning: Some font shapes were not available, defaults substituted.
LaTeX Warning: Label(s) may have changed. Rerun to get cross-references right.
)
Output written on .../input.pdf (2 pages).
Transcript written on .../input.log.
[INFO] [makePDF] Rerun needed
Package hyperref Warning: Rerun to get /PageLabels entry.
LaTeX Warning: Label(s) may have changed. Rerun to get cross-references right.
[INFO] [makePDF] LaTeX run number 2
[INFO] [makePDF] LaTeX output
This is XeTeX, Version 3.141592653-2.6-0.999995 (TeX Live 2023/Debian) (preloaded format=xelatex)
restricted \write18 enabled.
entering extended mode
(.../input.tex
LaTeX2e <2023-11-01> patch level 1
L3 programming layer <2024-01-22>
(.../article.cls
Document Class: article 2023/05/17 v1.4n Standard LaTeX document class
(.../[system]
(.../xcolor.sty
(.../color.cfg)
(.../xetex.def)
(.../[system]
(.../geometry.sty
(.../keyval.sty)
(.../ifvtex.sty
(.../iftex.sty)))
(.../amsmath.sty
For additional information on amsmath, use the `?' option.
(.../amstext.sty
(.../amsgen.sty))
(.../amsbsy.sty)
(.../amsopn.sty))
(.../amssymb.sty
(.../amsfonts.sty))
(.../unicode-math.sty
(.../expl3.sty
(.../l3backend-xetex.def))
(.../unicode-math-xetex.sty
(.../xparse.sty)
(.../l3keys2e.sty)
(.../fontspec.sty
(.../fontspec-xetex.sty
(.../fontenc.sty)
(.../fontspec.cfg)))
(.../fix-cm.sty
(.../ts1enc.def))
(.../unicode-math-table.tex)))
(.../lmodern.sty)
(.../xeCJK.sty
(.../ctexhook.sty)
(.../xtemplate.sty)
(.../xeCJK.cfg))
(.../upquote.sty
(.../textcomp.sty))
(.../microtype.sty
(.../etoolbox.sty)
(.../microtype-xetex.def)
(.../microtype.cfg))
(.../setspace.sty)
(.../parskip.sty
(.../kvoptions.sty
(.../ltxcmds.sty)
(.../kvsetkeys.sty)))
(.../graphicx.sty
(.../graphics.sty
(.../trig.sty)
(.../graphics.cfg)))
(.../bookmark.sty
(.../hyperref.sty
(.../kvdefinekeys.sty)
(.../pdfescape.sty
(.../pdftexcmds.sty
(.../infwarerr.sty)))
(.../hycolor.sty)
(.../auxhook.sty)
(.../nameref.sty
(.../refcount.sty)
(.../gettitlestring.sty))
(.../pd1enc.def)
(.../intcalc.sty)
(.../puenc.def)
(.../url.sty)
(.../bitset.sty
(.../bigintcalc.sty))
(.../atbegshi-ltx.sty))
(.../hxetex.def
(.../stringenc.sty)
(.../rerunfilecheck.sty
(.../atveryend-ltx.sty)
(.../uniquecounter.sty)))
(.../bkm-dvipdfm.def))
(.../xurl.sty)
(.../input.aux)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(.../mt-LatinModernRoman.cfg)
(.../omllmm.fd)
(.../umsa.fd)
(.../mt-msa.cfg)
(.../umsb.fd)
(.../mt-msb.cfg)
LaTeX Font Warning: Font shape `TU/ARPLUKaiCN(0)/b/n' undefined
(Font) using `TU/ARPLUKaiCN(0)/m/n' instead on input line 96.
[1] [2] (.../input.aux)
LaTeX Font Warning: Some font shapes were not available, defaults substituted.
)
Output written on .../input.pdf (2 pages).
Transcript written on .../input.log.
